SUBJECT :MATHEMATICS FORM ONE
TOPIC : NUMBERS
A number is a mathematical object used to count, measure and also label. The original examples are the natural numbers 1, 2, 3, 4 and so forth. ... Calculations with numbers are done with arithmetical operations, the most familiar being addition, subtraction, multiplication, division, and exponentiation
we know that when we count we start 1,2 .... . But there are other numbers like 0, negative numbers and decimals. All these types of numbers are categorized in different groups like counting numbers, integers,real numbers, whole numbers and rational and irrational numbers according to their properties. all this have been covered in this chapter
Natural and Whole Number
Natural numbers are counting numbers. Counting always starts with 1 and continues with 2, 3 … (dots means numbers continue with no end). Therefore Natural or counting numbers starts from 1 and continue to infinite (no end).
Natural numbers are denoted by N. natural numbers can be represented on a horizontal line called number line as shown above:
The other group of numbers starts from zero and it is called whole numbers denoted by W.
We can represent whole numbers on a number line as shown above:
The Difference between Natural and Whole Numbers
Distinguish between natural and whole numbers
Natural numbers are either used to count one to one objects or represent the position of an object in a sequence. They start from one and go on to infinity.This is why they are sometimes referred to as counting numbers. The only whole number that cannot be classified as a natural number is 0. Counting numbers can further be classified into perfect numbers, composite numbers, co-prime/ relatively prime numbers, prime numbers, even and odd numbers.
Even ,Odd, and Prime Numbers
Identify even ,odd, and prime numbers
Even numbers are those numbers which are divisible by 2. In other words we can say that any natural number which can be divided by 2 is an even number. For example 2, 4, 6, 8, 10, 12, … are even numbers since they are divisible by 2.
Odd numbers are those numbers which are not divisible by 2. In other words we can say that any natural number when divided by 2 and remains 1 including 1 are called odd numbers. Example 1, 3, 5, 7, 9, 11, 13, 15, … are called odd numbers.
Prime numbers are those numbers which are divisible by one and itself excluding one or any natural number which is divisible by one and itself except one. For example 2, 3, 5, 7, 11, 13, 17, … are called prime numbers.
Odd and Prime Numbers on Numbers Lines
Show even , odd and prime numbers on number lines
Odd and Prime Numbers
Operations with Whole Numbers
We have four operations which are: addition (+), subtraction (-), multiplication ( X) and division (÷).
Addition of Whole Numbers
Add whole numbers
When adding numbers we add the corresponding digits in their corresponding place values and we start adding from the right side i.e. from the place value of ones to the next.
We can add numbers horizontally or vertically.
Horizontal addition
Example 5
- 972 + 18=
- 23 750 + 250 =
Solution
- 972 + 18 = 990
- 23 750 + 250 = 24 000
Vertical addition
Example 6
Subtraction of Whole Numbers
Subtract whole numbers
Subtraction is denoted by the sign (-). It is sometimes called minus. Subtraction is the opposite of addition. Subtraction also means reduce a number from certain number and the answer that is obtained is called difference..
Subtraction is done in similar way like addition. We subtract the corresponding digits in their corresponding place value. For example; 505 – 13. We first subtract ones, which are 5 and 3. Subtract3 from 5 gives 2. Followed by tens which are 0 and 1. Subtract 1 from 0 is not possible. In order to make it easy, take 1 from 5 (hundreds). When 1 is added to 0 it has to be changed to be tens since it is added to a place of tens. So, when 1 comes into a place of tens it becomes 10. So add 10 to 0. We get 10. Now, subtract 1 from 10. We get 9. We are left with 4 in a place of hundreds since we took 1. There for our answer will be 492.
Note that similar manner will be used when subtracting.
Example 7
Multiplication of Whole Numbers
Multiply whole numbers
Multiplication means adding repeatedly depending on the times number given. For example; 25 6 means add 25, repeat adding 6 times i.e. 25 + 25 + 25 + 25 +25 + 25 = 150. The answer obtained after multiplying two or more numbers is called product. The number being multiplied is called a multiplicand while the number used in multiplying is called a multiplier. Referring our example, 25 is multiplicand and 6 is multiplier.
Example 8
Division of Whole Numbers
Divide whole numbers
Division is the same as subtraction. You subtractdivisor(the number used to divide another number) fromdividend(the number which is to be divided), we repeat subtracting divisor to the answer obtained until we get zero. The answer is how many times you repeat subtraction.
For example; 27 ÷9, we take 27 we subtract 9, we get 18. Again we take 18 we subtract 9, we get 9. We take 9 we subtract 9 we get 0. We repeat subtraction three times. Therefore the answer is 3. The answer obtained is calledquotient. Referring to our example; 27 is dividend, 9 is divisor and 3 is quotient. If a number can’t be divided exactly, what remains or left over is calledremainder.
Example 9
The Four Operations in Solving Word Problems
Use the four operations in solving word problems
Sometimes you may be given a question with mixed operations +, -, xand ÷ . We do multiplication and division first then addition and subtraction.
Example 10
- 12 ÷ 4 + 3 x 5
- 14 x2 ÷ 7 – 3 + 6
Solution
- 12 x 4 + 3 x 5 =3 + 15 (do division and multiplication fist) =18
- 14 x 2 ÷ 7 – 3 + 6 =28 ÷ 7 - 3 + 6 (multiply first) =4 – 3 + 6 (then divide) =10 – 3 (add then subtract) =7
We may use brackets to separate x,÷ , + and – if they are mixed in the same problem and use what is called BODMAS . BODMAS is the short form of the following:
B for Brackets O for Open D for Division M for Multiplication A for Addition and S for Subtraction
Therefore, with mixed operations, we first do the operation inside the brackets; we say that we open the brackets. Then we do division followed by multiplication, addition and lastly subtraction.
Example 11
Word problems on whole numbers
Example 12
In a school library there are 6 shelves each with 30 books. How many books are there?
Solution
Each shelf has 30 books
6 shelves have 30 × 6 = 180 books.
Therefore, there are 180 books.
Example 13
Juma’s mother has a garden with Tomatoes, Cabbages and Water Lemons. There are 4 rows of Tomato each with 30 in it. 6 rows of Cabbages with 25 in each and 3 rows of Water Lemo
Solution
There are 30 Tomatoes in each row
4 rows will have 30 × 4 = 120 Tomatoes
Each row has 25 Cabbages
6 rows have 25 × 6 = 150 Cabbages
Each row has 15 Water Lemons
3 rows have 15 × 3 = 45 Water Lemons
In total there 120 + 150 + 45 = 315 plants.
Therefore in Juma’s mother garden there are 315 plants.
Example 14
A school shop collects sh 90 000 from customers each day. If sh 380 000 from the collection of 6 days was used to buy books. How much money was left?
Each day the collection is sh 90 000
6 days collection is sh 90 000 × 6 = sh 540 000
The money left will be = Total collection – Money used
= sh 540 000 – sh 380 000 = sh 160 000
Therefore the money left was sh 160 000
Exercise 1
1. For each of the following numbers write the place value of a digit in a bracket.
- 899 482 (4)
- 1 940 (0)
- 9 123 476
2. Write the numerals for each of the following problems.
- Ten thousand and fifty one.
- Nine hundred thirty millio
Factors And Multiples Of Numbers
Factors of a Number
Find factors of a number
Consider two numbers 5 and 6, when we multiply these numbers i.e. 5 6 the answer is 30. The numbers 5 and 6 are called factors or divisors of 30 and number 30 is called a multiple of 5 and 6. Therefore factors are the divisors of a number.
Example 15
Find all factors of 12
Note that, when listing the factors we don’t repeat any of it.
Multiples of a Number
Find multiples of a number
Multiples of a number are the products of a number. For example multiples of 4 are 4, 8, 12, 16, 20, 24, … This means multiply 4 by 1, 2, 3, 4, 5, 6, … .
Example 16
Example
List all multiples of 6 between 30 and 45.
Solution
The multiples of 6 are: 6×1 = 6; 6×2 = 12; 6×3 = 18; 6×4 = 24; 6×5 = 30; 6×6 = 36; 6×7 = 42; 6×8 = 48 and so on.
Therefore, multiples of 6 between 30 and 45 are 36 and 42.
Factors to Find the Greatest Common Factors(GCF) of Numbers
Use factors to find the greatest common factors(GCF) of numbers
Greatest Common Factor is sometimes called Highest Common Factor. Its short form is (GCF) or (HCF) respectively. The Greatest Common Factor is the largest common divisor of two or more numbers given.
For example if you are told to find the GCF of 15 and 25. First, list all factors or divisors of 15 and that of 25. Thus, factors of 15 are 1, 3, 5, 15factors of 25 are 1, 5, 25
The common factors are 1 and 5. Therefore the GCF is 5.
Example 17
Example1
Find the HCF of 72 and 120.
Solution
We have to list factors of our numbers:
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The common factors are 1, 2, 3, 4, 6, 8, 12, 24.
Therefore the HCF of 72 and 120 is 24.
Another method which can be used to find the GCF or HCF is prime factorization method.
Example 18
Example
Find the HCF of 36 and 48.
Solution
We have to find prime factors of 36 and 48 first
thus, 36 = 2×2×3×3.
48 = 2×2×2× 2×3.
After writing the numbers as a product of their prime factors, take only the common prime factors (prime factors appeared to all numbers). In our example the common factors are 2×2×3. Therefore the HCF of 36 and 48 is 12.
Lowest Common Multiple (LCM)
Lowest Common Multiple is also called Least Common Multiple and its short form is LCM.For example: multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, …multiples of 3 are 3, 9, 15, 18, 21, 24, 27, 30, 33, ….
When you look carefully at these multiples of 5 and 3 you notes that 15 had appeared to both. This multiple which appear to both is called a common multiple. If there are more than one common multiples which appeared the smaller common multiple is what is called Lowest Common Multiple.
Example 19
Find the common multiples and then show the Lowest Common Multiple of the numbers 4, 6 and 8.
Solution
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, …
Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, …
The common multiples of 4, 6 and 8 are 24, 48, …
Therefore the Lowest Common Multiple of 4, 6, and 8 is 24.
We can find the Lowest Common Multiple (LCM) of numbers by writing the numbers as a product of their prime factors. The method is called prime factorization.
Example 20
Find the LCM of 24 and 36 by prime factorization method.
Solution
Let us find prime factors of each number by dividing the numbers by their prime factors.
Now take the prime factors which appear to both numbers i.e. 2×2×3 (we take without repeating). We are left with 2 which is a multiple of 24 and 3 which is a multiple 36. We have also to multiply these prime factors left i.e. 2×2×2×3×3. This gives 72. Therefore the LCM of 24 and 36 is 2×2×2×3×3= 72.
Integers
Identify integers
Consider a number line below
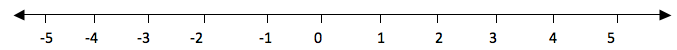
The numbers from 0 to the right are called positive numbers and the numbers from 0 to the left with minus (-) sign are called negative numbers. Therefore all numbers with positive (+) or negative (-) sign are called integers and they are denoted by Ζ. Numbers with positive sign are written without showing the positive sign. For example +1, +2, +3, … they are written simply as 1, 2, 3, … . But negative numbers must carry negative sign (-). Therefore integers are all positive and negative numbers including zero (0). Zero is neither positive nor negative number. It is neutral.
The numbers from zero to the right increases their values as the increase. While the numbers from zero to the left decrease their values as they increase. Consider a number line below.
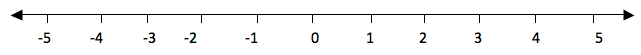
If you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater than 2. We use the symbol ‘>’ to show that the number is greater than i. e. 3 >2(three is greater than two). And since 2 is to the left of 3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is use to show that the number is less than.
Consider numbers to the left of 0. For example if you take -5 and -3. -5 is to the left of -3, therefore -5 is smaller than -3. -3 is to the right of -5, therefore -3 is greater than -5.
Generally, the number which is to the right of the other number is greater than the number which is to the left of it.
If two numbers are not equal to each to each other, we use the symbol ‘≠’ to show that the two numbers are not equal. The not equal to ‘≠’ is the opposite of is equal to ‘=’.
Example 21
Represent the following integers Ζ on a number line
- 0 is greater than Ζ and Ζ is greater than -4
- -2 is less than Ζ and Ζ is less than or equal to 1.
Solution
a. 0 is greater than Ζ means the integers to the left of zero and Ζ is greater than -4 means integers to the left of -4. These numbers are -1, -2 and -3. Consider number line below
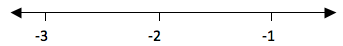
b. -2 is less than Ζ means integers to the right of -2 and Ζ is less than or equal to 1 means integers to the left of 1 including 1. These integers are -1, 0 and 1. Consider the number line below
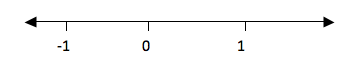
Example 22
Put the signs ‘is greater than’ (>), ‘is less than’ (<), ‘is equal to’ (=) to make a true statement.
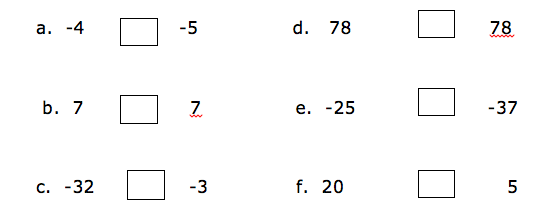
Addition of Integers
Add integers
Example 23
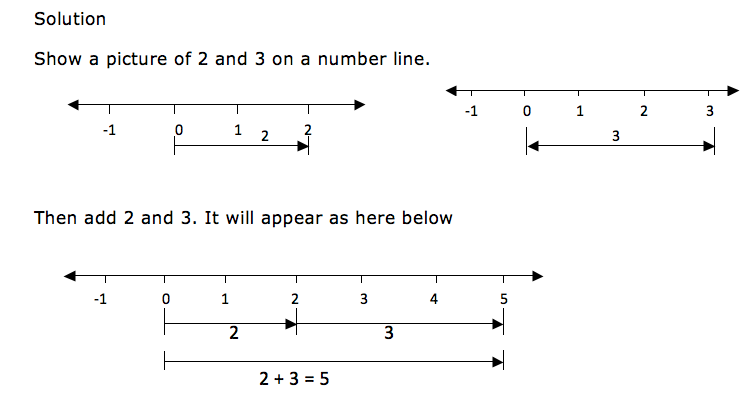
2 + 3
Show a picture of 2 and 3 on a number line.
When drawing integers on a number line, the arrows for the positive numbers goes to the right while the arrows for the negative numbers goes to the left. Consider an illustration bellow.
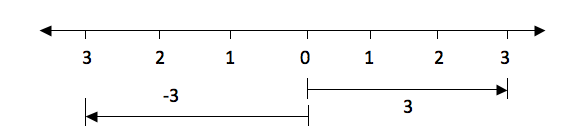
The distance from 0 to 3 is the same as the distance from 0 to -3, only the directions of their arrows differ. The arrow for positive 3 goes to the right while the arrow for the negative 3 goes to the left.
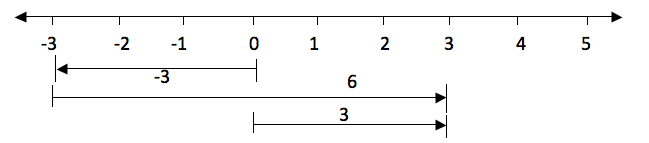
Example 24
-3 + 6
Solution
Subtraction of Integers
Subtract integers
Since subtraction is the opposite of addition, if for example you are given 5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can use a number line in the same way as we did in addition. Therefore 5-4 on a number line will be:
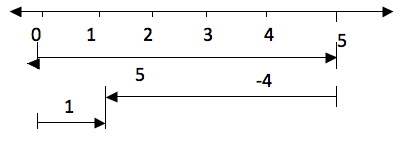
Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.
Multiplication of Integers
Multiply integers
Example 25
2×6 is the same as add 2 six times i.e. 2×6 = 2 + 2 + 2 + 2 + 2 +2 = 12. On a number line will be:
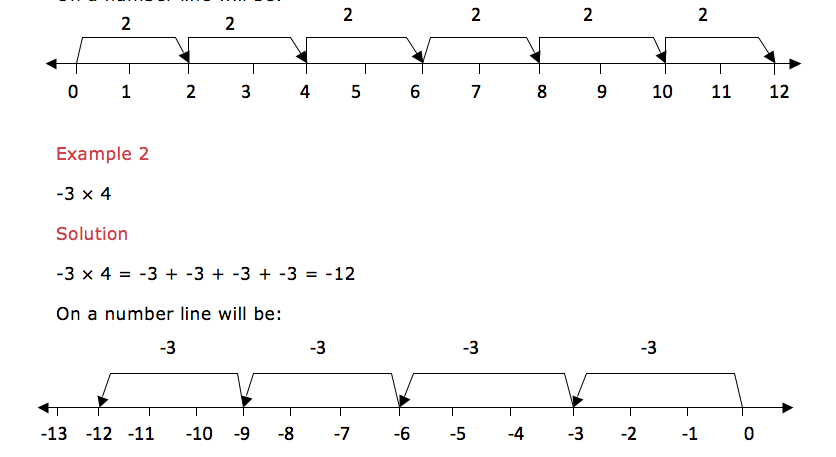
Multiplication of a negative integer by a negative integer cannot be shown on a number line but the product of these two negative integers is a positive integer.
From the above examples we note that multiplication of two positive integers is a positive integer. And multiplication of a positive integer by a negative integer is a negative integer. In summary:
- (+)×,(+) = (+)
- (-)×,(-) = (+)
- (+)×,(-) = (-)
- (-)×,(+) = (-)
Division of Integers
Divide integers
Example 26
6÷3 is the same as saying that, which number when you multiply it by 3 you will get 6, that number is 2, so, 6÷3 = 2.
Therefore division is the opposite of multiplication. From our example 2×3 = 6 and 6÷3 = 2. Thus multiplication and division are opposite to each other.
Dividing two integers which are both positive the quotient (answer) is a positive integer. If they are both negative also the quotient is positive. If one of the integer is positive and the other is negative then the quotient is negative. In summary:
- (+)÷(+) = (+)
- (-)÷(-) = (+)
- (+)÷(-) = (-)
- (-)÷(+) = (-)
Mixed Operations on Integers
Perform mixed operations on integers
You may be given more than one operation on the same problem. Do multiplication and division first and then the rest of the signs. If there are brackets, we first open the brackets and then we do division followed by multiplication, addition and lastly subtraction. In short we call it BODMAS. The same as the one we did on operations on whole numbers.
Example 27
9÷3 + 3×2 -1 =
Solution
9÷3 + 3×2 -1
=3 + 6 -1 (first divide and multiply)
=8 (add and then subtract)
Example 28
(12÷4 -2) + 4 – 7=
Solution
(12÷4 -2) + 4 – 7
=1 + 4 – 7 (do operations inside the brackets and divide first)
=5 – 7 (add)
=2
TOPIC 2: FRACTIONS
A fraction is a number which is expressed in the form of a/b where a - is the top number called numerator and b- is the bottom number called denominator.
A Fraction
Describe a fraction
A fraction is a number which is expressed in the form of a/b where a - is the top number called numerator and b- is the bottom number called denominator.
Consider the diagram below
The shaded part in the diagram above is 1 out of 8, hence mathematically it is written as 1/8
Example 1
(a) 3 out of 5 ( three-fifths) = 3/5
Example 2
(b) 7 0ut of 8 ( i.e seven-eighths) = 7/8
Example 3
- 5/12=(5 X 3)/(12 x 3) =15/36
- 3/8 =(3 x 2)/(8 X 2) = 6/16
Dividing the numerator and denominator by the same number (This method is used to simplify the fraction)
Difference between Proper, Improper Fractions and Mixed Numbers
Distinguish proper, improper fractions and mixed numbers
Proper fraction -is a fraction in which the numerator is less than denominator
Example 4
4/5, 1/2, 11/13
Improper fraction -is a fraction whose numerator is greater than the denominator
Example 5
12/7, 4/3, 65/56
Mixed fraction -is a fraction which consist of a whole number and a proper fraction
Example 6
(a) To convert mixed fractions into improper fractions, use the formula below
(b)To convert improper fractions into mixed fractions, divide the numerator by the denominator
Example 7
Convert the following mixed numbers into improper fractions
Comparison of Fractions
In order to find which fraction is greater than the other, put them over a common denominator, and then the greater fraction is the one with greater numerator.
A Fraction to its Lowest Terms
Simplify a fraction to its lowest terms
Example 8
For the pair of fractions below, find which is greater
Solution
Equivalent Fractions
Identify equivalent fractions
Equivalent Fraction
- Are equal fractions written with different denominators
- They are obtained by two methods
<!-- [if !supportLists]-->(a) <!--[endif]-->Multiplying the numerator and denominator by the same number
<!-- [if !supportLists]-->(a) <!--[endif]-->Dividing the numerator and denominator by the same number (This method is used to simplify the fraction
NOTE: The fraction which cannot be simplified more is said to be in its lowest form
Example 9
Simplify the following fractions to their lowest terms
Solution
Fractions in Order of Size
Arrange fractions in order of size
Example 10
Arrange in order of size, starting with the smallest, the fraction
Solution
Put them over the same denominator, that is find the L.C.M of 3, 7, 8 and 9
Addition of Fractions
Add fractions
Operations on fractions involves addition, subtraction, multiplication and division
- Addition and subtraction of fractions is done by putting both fractions under the same denominator and then add or subtract
- Multiplication of fractions is done by multiplying the numerator of the first fraction with the numerator of the second fraction, and the denominator of the first fraction with the denominator the second fraction.
- For mixed fractions, convert them first into improper fractions and then multiply
- Division of fractions is done by taking the first fraction and then multiply with the reciprocal of the second fraction
- For mixed fractions, convert them first into improper fractions and then divide
Example 11
Find
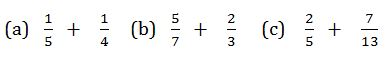
Solution
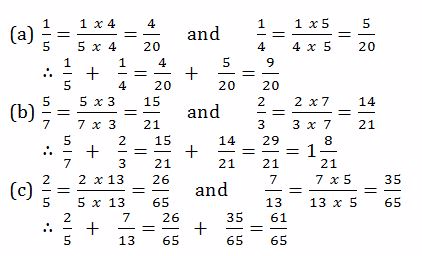
Subtraction of Fractions
Subtract fractions
Example 12
Evaluate
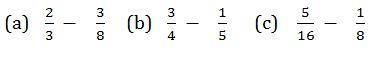
Solution
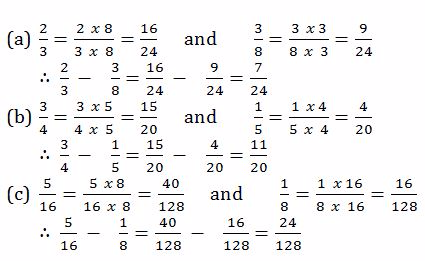
Multiplication of Fractions
Multiply fractions
Example 13
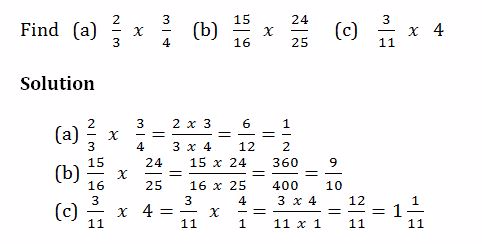
Division of Fractions
Divide fractions
Example 14
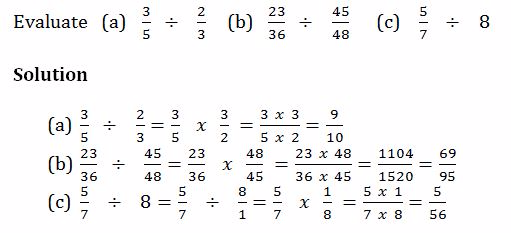
Mixed Operations on Fractions
Perform mixed operations on fractions
Example 15
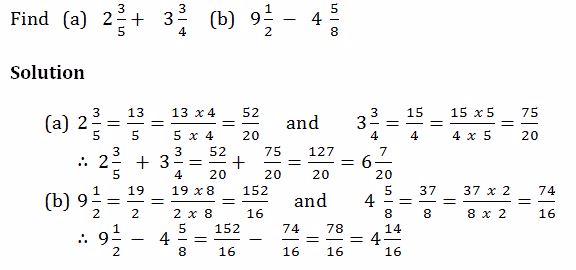
Example 16
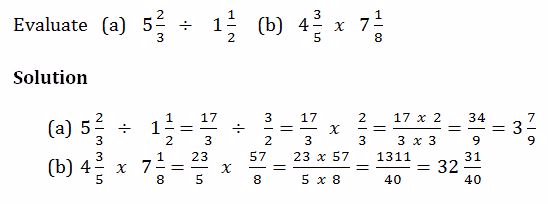
Word Problems Involving Fractions
Solve word problems involving fractions
Example 17
- Musa is years old. His father is 3¾times as old as he is. How old is his father?
- 1¾of a material are needed to make suit. How many suits can be made from
TOPIC 3: DECIMAL AND PERCENTAGE
The Concept of Decimals
Explain the concept of decimals
A decimal- is defined as a number which consist of two parts separated by a point.The parts are whole number part and fractional part
Example 1
Example 2
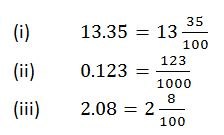
Conversion of Fractions to Terminating Decimals and Vice Versa
Convert fractions to terminating decimals and vice versa
The first place after the decimal point is called tenths.The second place after the decimal point is called hundredths e.t.c
Consider the decimal number 8.152
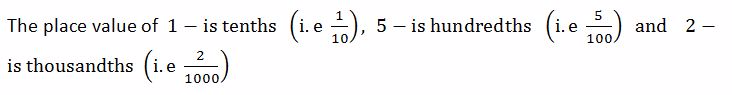
NOTE
- To convert a fraction into decimal, divide the numerator by denominator
- To convert a decimal into fraction, write the digits after the decimal point as tenths, or hundredths or thousandths depending on the number of decimal places.
Example 3
Convert the following fractions into decimals
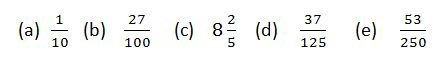
Solution
Divide the numerator by denominator
Operations and Decimals
Addition of Decimals
Add decimals
Example 4
Evaluate
Solution
Subtraction of Decimals
Subtract decimals
Example 5
Solution
Multiplication of Decimals
Multiply decimals
Example 6
Solution
Mixed Operations with Decimals
Perform mixed operations with decimals
Example 7
Solution
Word Problems Involving Decimals
Solve word problems involving decimals
Example 8
If 58 out of 100 students in a school are boys, then write a decimal for the part of the school that consists of boys.
Solution
We can write a fraction and a decimal for the part of the school that consists of boys.
| fraction | decimal |
| 58/100 | 0.58 |
Expressing a Quantity as a Percentage
Express a quantity as a percentage
The percentage of a quantity is found by converting the percentage to a fraction or decimal and then multiply it by the quantity.
Example 9
NOTE:The concept of percentage of a quantity can be used to solve the problems involving percentage increase and decrease as shown in the below examples:-
A Fractions into Percentage and Vice Versa
Convert a fraction into percentage and vice versa
To change a fraction or a decimal into a percentage, multiply it by 100%
Example 10
Convert the following fractions into percentages
A Decimal into Percentage and Vice Versa
Convert a decimal into percentage and vice versa
To change a percentage into a fraction or a decimal, divide it by 100%
Example 11
Convert the following percentages into decimals
Percentages in Daily Life
Apply percentages in daily life
Example 12
In an assignment, Regina scored 9 marks out of 12. Express this as a percentage
Solution
Example 13
A school has 400 students of which 250 are girls. What percentage of the students are not girls?
Solution
Hello, my name is Jack Sparrow. I'm a 50 year old self-employed Pirate from the Caribbean.
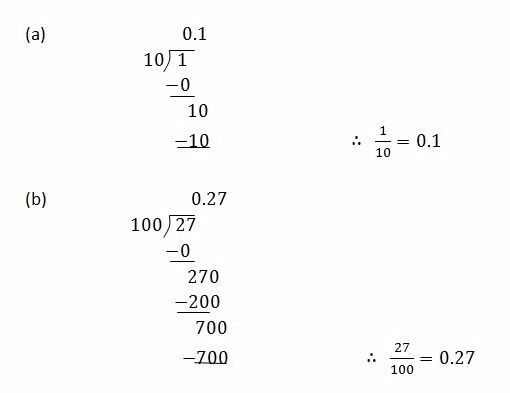
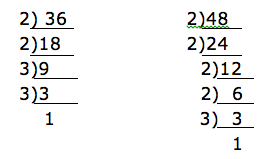
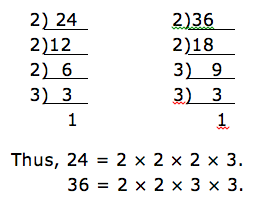
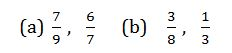
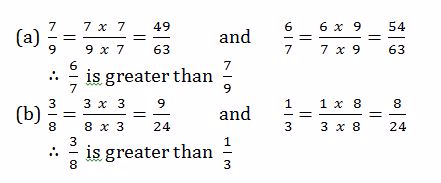
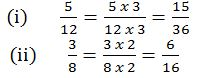
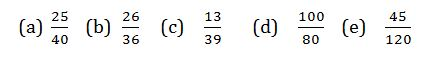
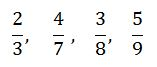
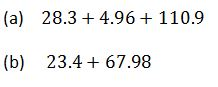
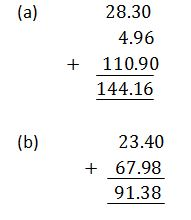
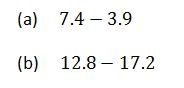
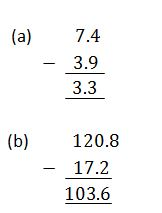
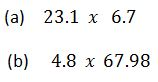
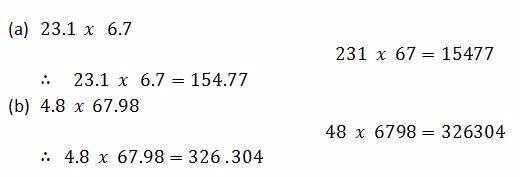
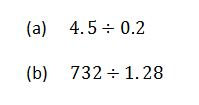
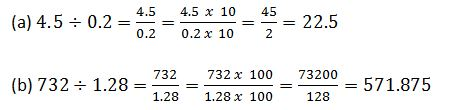
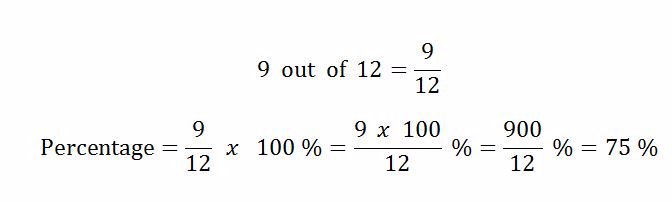
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.