Concept of Exponent from School Kwanza academy|Mwl.Jerome Massawe
Exponent how many times to use the number in a multiplication.
Exponent of
number Says how many times to use the number in a
multiplication.
Number(base)
42 = 4x4
42 ,4 to 2 exponents
The
exponent of a number says how many times to use that number in a
multiplication.
It is written as a small number to the right and above the base number.
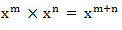
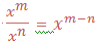
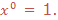
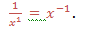
In this example: 82 = 8 × 8 = 64
(The exponent "2" says to use the 8 two times in a multiplication.)
Another example: 53 = 5 × 5 × 5 = 125
(The exponent "3" says to use the 5 three times in a multiplication.)
Other names for exponent are index or power.
multiplication.
It is written as a small number to the right and above the base number.
The Laws of Exponents
First law:Multiplication of positive integral exponent
State that the base remain in (unity) or same but power added
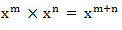
Second law: Division of positive integral exponent
State that the base remain in (unity) or same but power numerator power minus denominator power
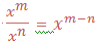
Third law: Zero exponents
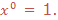
Fourth law: Negative integral exponents
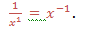
In this example: 82 = 8 × 8 = 64
(The exponent "2" says to use the 8 two times in a multiplication.)
Another example: 53 = 5 × 5 × 5 = 125
(The exponent "3" says to use the 5 three times in a multiplication.)
Other names for exponent are index or power.
Example:
The exponent of
a number says how many times to use the number in a
multiplication.
In 82 the
"2" says to use 8 twice in a multiplication,
so 82 = 8 × 8 = 64
so 82 = 8 × 8 = 64
In words: 82 could
be called "8 to the power 2" or "8 to the second power", or
simply "8 squared"
Exponents
are also called Powers or Indices.
Some more examples:
Example: 53 = 5 × 5 × 5 = 125
·
In words: 53 could be called "5 to the third
power", "5 to the power 3" or simply "5 cubed"
Example: 24 = 2 × 2 × 2 × 2 = 16
·
In words: 24 could be called "2 to the
fourth power" or "2 to the power 4" or simply "2 to the
4th"
Exponents make it easier to
write and use many multiplications
Example: 96 is
easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
You can
multiply any number by itself as many times as
you want using exponents.
Try here:
In General
So in general:
an tells
you to multiply a by itself,
so there are n of those a's: |
 |
Other Way
of Writing It
Sometimes people use
the ^ symbol (above the 6 on your keyboard), as it is easy to
type.
Example: 2^4 is the same as 24
·
2^4 = 2 × 2 × 2 × 2 = 16
Negative
Exponents
Negative? What could be the
opposite of multiplying?
Dividing!
A negative exponent means
how many times to divide one by the number.
Example: 8-1 =
1 ÷ 8 = 0.125
You can have many divides:
Example: 5-3 =
1 ÷ 5 ÷ 5 ÷ 5 = 0.008
But that can be done an
easier way:
5-3 could also be
calculated like:
1 ÷ (5 × 5 × 5) = 1/53 =
1/125 = 0.008
In General
 |
That last example showed
an easier way to handle negative exponents:
·
Calculate the positive exponent (an)
|
More Examples:
Negative Exponent
|
Reciprocal of Positive Exponent
|
Answer
|
||
4-2
|
=
|
1
/ 42
|
=
|
1/16
= 0.0625
|
10-3
|
=
|
1
/ 103
|
=
|
1/1,000
= 0.001
|
(-2)-3
|
=
|
1
/ (-2)3
|
=
|
1/(-8)
= -0.125
|
What if the
Exponent is 1, or 0?
1
|
If the exponent is 1, then you just have the number itself
(example 91 = 9)
|
|
0
|
If the exponent is 0, then you get 1 (example 90 = 1)
|
|
But what about 00 ? It could be
either 1 or 0, and so people say it is "indeterminate".
|
It All
Makes Sense
My favorite method is to
start with "1" and then multiply or divide as many times as the
exponent says, then you will get the right answer, for example:
Example:
Powers of 5
|
|||
..
etc..
|
|||
52
|
1 × 5 × 5
|
25
|
|
51
|
1 × 5
|
5
|
|
50
|
1
|
1
|
|
5-1
|
1 ÷ 5
|
0.2
|
|
5-2
|
1 ÷ 5 ÷ 5
|
0.04
|
|
..
etc..
|
|||
If you look at that table,
you will see that positive, zero or negative exponents are really part of the
same (fairly simple) pattern.
Be Careful
About Grouping
To avoid confusion, use
parentheses () in cases like this:
With
() :
|
(-2)2 = (-2) × (-2) = 4
|
Without
() :
|
-22 = -(22) = - (2 × 2) = -4
|
With
() :
|
(ab)2 = ab × ab
|
Without
() :
|
ab2 = a × (b)2 = a × b × b
|







No comments:
Post a Comment
Note: Only a member of this blog may post a comment.